Дифференциальные уравнения — это фундаментальный инструмент математики, который связывает значения функции с ее производными, помогая моделировать реальные процессы от колебаний до роста популяций. В российском образовании они изучаются на факультетах математики, прикладной математики и информатики в вузах вроде МГУ, МФТИ или СПбГУ, где студенты осваивают их как основу для инженерных и научных специальностей. Здесь стоит сразу отметить, что без понимания видов уравнений трудно перейти к методам решения, так что разберем это шаг за шагом, чтобы было понятно даже тем, кто только начинает.
Сначала о базовой классификации: все дифференциальные уравнения делятся на обыкновенные (ОДУ), где функция зависит от одной переменной, и уравнения с частными производными (УРЧП), которые работают с несколькими переменными — это как разница между прямой дорогой и лабиринтом с поворотами. ОДУ чаще всего встречаются на первом курсе, а УРЧП — уже на более продвинутых этапах, например, в мехмате МГУ. Еще есть стохастические ДУ, но они реже, в основном для экономистов или физиков в РАНХиГС или НГУ. Линейные уравнения проще в решении, потому что неизвестная функция и производные не перемножаются, в отличие от нелинейных, которые могут быть настоящей головоломкой — подумайте, как нелинейность усложняет прогнозирование погоды.
Переходя к ОДУ первого порядка, которые часто становятся первыми “врагами” студентов. Уравнения с разделяющимися переменными — это когда можно разнести все по полочкам: левая часть только от x, правая — от y. Например, в типичном задании из учебника Демидовича, который все помнят по сессиям, вы интегрируете по отдельности, и вуаля, решение готово. Это хороший вариант для начинающих, потому что метод прямолинейный, без лишних хитростей, хотя иногда приходится бороться с логарифмами или тригонометрией.
Однородные уравнения — еще один популярный тип, где функции в правой части имеют одинаковую степень. Замена y = vx превращает их в разделяющиеся, и это как волшебный ключ: в вузах вроде Бауманки учат именно так, чтобы студенты могли быстро применять на практике. А вот уравнения Бернулли, с их y^n в нелинейной части, требуют замены v = y^{1-n}, чтобы свести к линейному — здесь стоит обратить внимание на знаки, иначе ошибка выльется в неверное решение. В линейных ОДУ первого порядка коэффициенты могут быть постоянными или переменными, и метод интегрирующего множителя спасает ситуацию; это базис для многих прикладных задач в экономике или биологии.
Для второго порядка все усложняется, но в российском образовании акцент на линейных уравнениях с постоянными коэффициентами — их решают через характеристическое уравнение, и корни определяют, будет ли решение экспонентой или синусом. Непосредственное интегрирование работает, если одна переменная отсутствует, а для неоднородных добавляется частное решение. В вузах типа Томского политеха студенты проходят это с примерами из механики, где уравнения описывают колебания пружины.
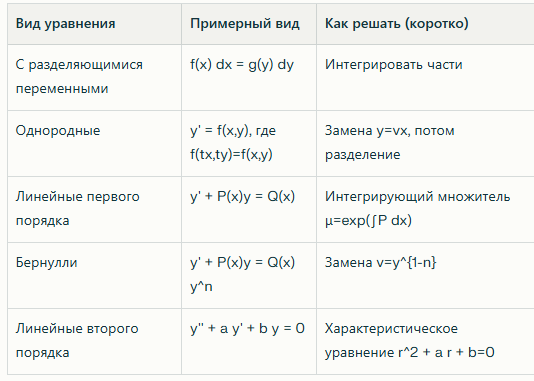
Таблица основных видов ОДУ и методов
Эта таблица — не строгий учебник, а скорее шпаргалка, чтобы быстро сориентироваться; в реальности для каждого вида есть нюансы, зависящие от коэффициентов. Обратите внимание, что в неидеальных случаях, как с переменными коэффициентами, приходится использовать ряды Тейлора или численные методы, которые в МФТИ преподают на параллельных курсах.
В общем, дифференциальные уравнения — это не просто формулы, а способ понять, как мир меняется, и в российском образовании они открывают двери в мехмат, прикладную математику или даже IT-специальности вроде data science в ВШЭ. Если вы студент, не бойтесь практики: решайте задачи из сборников, и все встанет на места. А для тех, кто выбирает профессию, знание этих видов — ключ к карьере в науке или инженерии, где без них никуда.